Bahas Soal Matematika   »     ›  

Tentukan hasil dari \( \int \frac{x^5-3}{x^3-x} \ dx = \cdots \ ? \)

Pembahasan:

Perhatikan bahwa fungsi dalam integralnya merupakan fungsi rasional tidak sejati di mana pangkat pembilang polinom lebih besar dari pangkat penyebut sehingga dilakukan pembagian polinom terlebih dahulu, diperoleh:

Dari hasil di atas, untuk integral yang pertama dapat dikerjakan dengan rumus dasar integral, yakni:

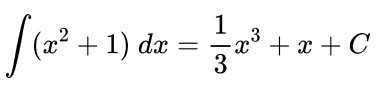
Selanjutnya, untuk integral yang kedua, fungsi dalam integralnya merupakan fungsi rasional sejati di mana pangkat pembilang lebih kecil dari pangkat penyebut. Fungsi pada penyebut dapat diuraikan menjadi faktor linear yang berlainan, yaitu:

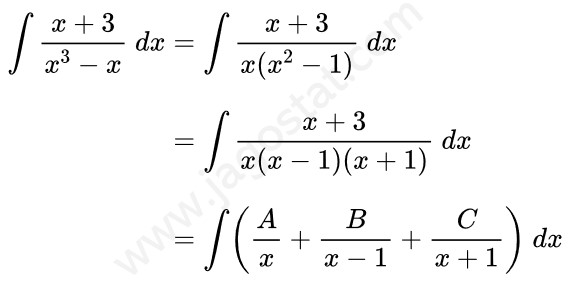
Sekarang kita akan mencari nilai A, B, dan C sebagai berikut:

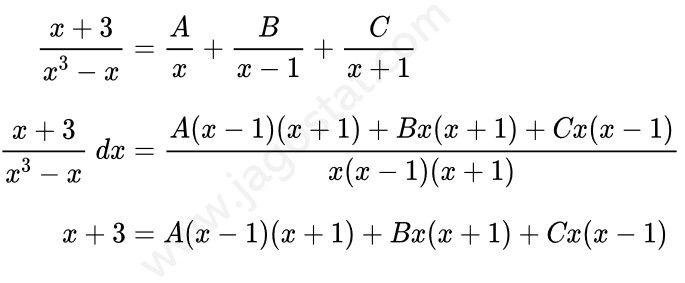
Dari hasil di atas, kita akan mengambil sembarang nilai \(x = -1, 0, 1 \) untuk memperoleh nilai A, B, dan C.

Dengan demikian, diperoleh:

Jadi, hasil dari \( \int \frac{x^5-3}{x^3-x} \ dx \) adalah